Implicit neural representation: Chaotic signals and Turing patterns

It’s always the road less travelled that makes the difference. Today’s post is a bit different. This week I am sharing an interesting road taken by researchers from Stanford and my experimentation with it. These are original experimental results not published elsewhere.

I came across the work of Vincent Sitzmann et. al (Website ) on SIREN from the tweet of Prof. Geoffrey Hinton, the father of deep learning.

Geoffrey Hinton @geoffreyhinton

A non-linearity that works much better than ReLUs. The work described in this video might also be relevant to understanding grid cells.

youtube.comImplicit Neural Representations with Periodic Activation Functions-- Project page -- https://vsitzmann.github.io/siren -- arXiv preprint -- https://arxiv.org/abs/2006.09661 -- Abstract -- Implicitly defined, continuous, dif...

Implicit Neural Representations with Periodic Activation Functions

The paper talks about a new activation function which can revolutionise the performance of Deep Learning Networks. This is a new way of thinking when it comes to handling data for deeplearning.

So let’s get to understand this. Assume that we have an image (x,y pixels) with three colours RGB. The task here is to find a function which can map (x,y) to (RGB) i.e. (R,G,B) = Φ(x,y).

In the traditional approach, we have to train a network to replace Φ. We can do this by building an n-layer fully connected neural network with a nonlinear activation function. The most common activation functions are: ReLU, Leaky ReLU, tanhx, sigmoid.

There can be another way of doing that and this is what this paper talks about.

Implicit Representation

In case of implicit representation, you train the network with one image and not with a series of images and arrive at a set of parameters which represent that image. This means one image can be an entire datasets that helps you arrive at Φ.

How does implicit representation help?

Compared to traditional network training, implicit representation provides us with continuous mapping from pixel value to a location and it can also learn (assign loss function to) gradients and Laplacian of the network.

The paper is very simple in its implementation. The authors have used sine as the non-linearity over any other non-linearity and that’s what made all the difference. In a few epochs, the decoded image starts reconstructing and after 200-300 epoch it’s almost a replica of the image.

Sample the following image both for RELU nonlinearity as well as sine nonlineaity for 500 epochs

Decoded Image, Gradient and Laplace with RELU as nonlinearity

Decoded Image, Gradient and Laplace with sine as nonlinearity

---

I went further and explores the same with turning patterns and the results are way better and reproducible with sine as nonlinearity.

What are turning patterns?

The idea of tinkering was to check if there is any change when it comes to use images which has patterns or even signals which are chaotic.

Input image

Decoded Image, Gradient and Laplace with RELU as nonlinearity

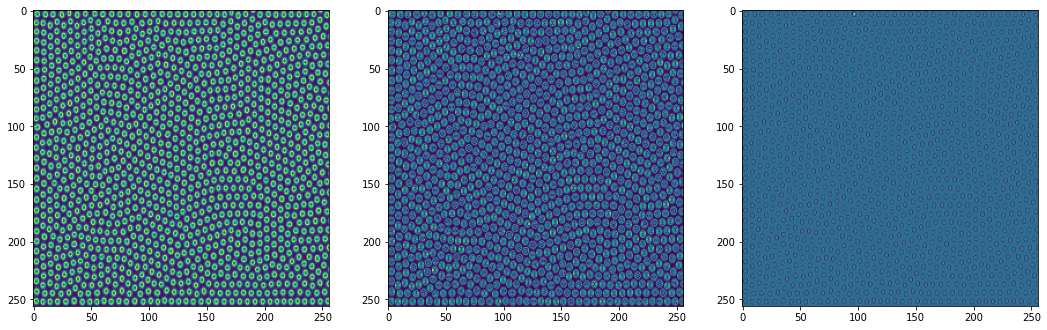
Decoded Image, Gradient and Laplace with sine as nonlinearity

I recommend you to go through the website and check various applications in audio, video, solving Poisson’s equation, Helmholz equation and Wave equation, and many others that are possible by simple replacement of nonlinearity in the implicit representation of an input dataset.

Website link: https://vsitzmann.github.io/siren/

---

As an example to have a implicit representation of a chaotic signal, I further experimented with Lorentz and Chua’s attractor.

Chaotic Systems

Chaotic system is the ones that show high sensitivity to initial conditions. In such systems, any uncertainty (no matter how small) in the beginning will produce rapidly escalating and compounding errors in the prediction of the system's future behaviour. What better to see such an effect than the corona crisis.

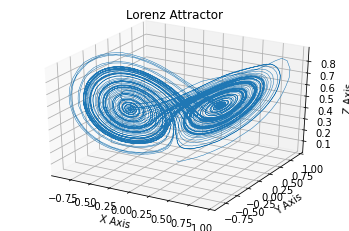
Lorentz Attractor

The Lorenz system is a system of ordinary differential equations and has chaotic solutions for certain parameter values and initial conditions. Lorentz system underscores that physical systems can be completely deterministic and yet still be inherently unpredictable. The equations describing the Lorentz system are:

here solution of the equation with σ = 10, ρ = 28 and β = 8/3 represents a state of chaos.

An attractor describes a state to which a dynamical system evolves after a long enough time. Systems that never reach this equilibrium are known as strange attractors.

Plotting x,y,z leads to the following result.

I have then passed these signals to three SIRENs and the outputs were then plotted.

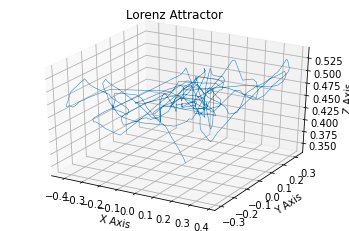
Lorentz System with RELU nonlinearity

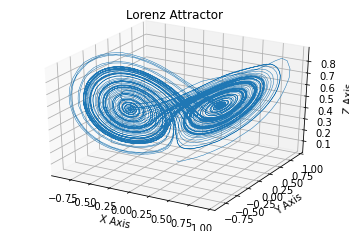
Lorentz System with sine nonlinearity

This clearly states how siren is the network architecture that succeeds in reproducing chaotic signals

Chua’s Circuit

Chua's circuit is a simple electronic circuit that exhibits classic chaotic behaviour. This means that it produces an oscillating waveform that, unlike an ordinary electronic oscillator, never "repeats". It was invented in 1983 by Prof. Leon O. Chua.

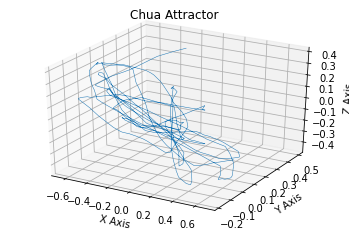
Chua’s circuit with RELU nonlinearity

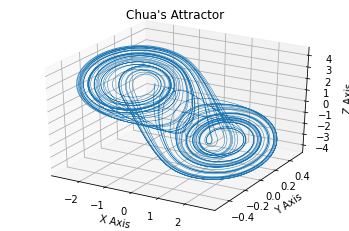
Chua’s circuit with sine nonlinearity

I am still studying the results and looking for suitable applications. If anyone has any immediate ideas or thoughts, please get in touch.

Read more:

1. Implicit Neural Representations with Periodic Activation Functions

2. Complete Guide of Activation Functions

3. SIRENs — Implicit Neural Representations with Periodic Activation Functions

4. Chua’s Circuit for High School Students

   Presentation

   ..coming up soon.

   Community

   Through this series, I intend to build a community of scientists, researchers, and doers. If you are pursuing an interesting research and want to share it with the community, please drop me a message.

   The idea behind the series is to share a community reading list and explore new ideas. This newsletter is a spin-off of an everyday AI session series where we picked one topic of AI a day and discussed that.

   Spread the word!