What are patterns and why should you care to know about them?

From stock markets to fake news detection, from beauty in painting to melody in music and from the spread of the epidemic to weather prediction, we are surrounded by patterns. We recognize a pattern and know it only when we see it.
Ever wondered what are patterns? Why are they the way they are? How can we detect patterns or even create them ? and more importantly, why should we?
Let’s start with some examples of patterns.
A. ) 1, 2, 4, 8, 16, 32, 64, _____
B.) sample this image

C.) or this broccoli

D.) Or a melody here

E.) Zebra stripes

In all the samples above, one may see a particular way in which something is done, is organized, or happens. This abstraction is called a pattern.
What is a pattern?
The pattern is an abstract concept that can be defined as a form of correlation between the states of an element within a system. In all of the above examples, one can break the system into elements and can draw the correlation between the state of the elements. In the first and fourth cases, the elements will have temporal correlation (elements are spaced in time; assuming one element represents one event in time) while in the other two its spatial (i.e. elements are spaced in geometry).
All systems exhibit some form of pattern which can be either spatial or temporal or both.
.. and what is correlation?
A correlation is a structured relationship between variables and in this case between the elements. Note the emphasis on structure. This means that a combination of correlation forms some pattern and if there is no correlation then we have a random pattern.
If we see around, we will find patterns and if we break down those patterns to elements we will find that it is the structured correlation between the elements that give rise to those patterns. In fact, our entire science is based on finding patterns, and to a large extent, mathematics can be treated as a science of patterns, if at all.
How does scientific process works?
A scientist tries to make a series of empirical observations and then tries to draw a relation between these observations. This correlation helps them find a pattern that helps in unravelling the mysteries of the universe.
Eureka is the moment of discovering the pattern :)
We, as a scientific and rational society, have been finding the correlation between various elements and have been unravelling the mysteries of nature for many centuries and this has intensified in recent years due to massive computations at our disposal.
Correlation:
Relationships between the elements can be further classified as:
The direction of the sign of correlation - which means either the relationship can be positive or negative.
Strength of correlation - which defines the coupling between the elements
The linearity of correlation - Linear relation means that the ratio of change between variables remains the same, which is nonlinear it is not the same.
Also, note that correlation does not imply causation. This means just because two things are correlated, it may not mean that one is causing the other. This is very important in the current context to detect certain types of fake news or exaggerated or even wrong claims.
Sample this :
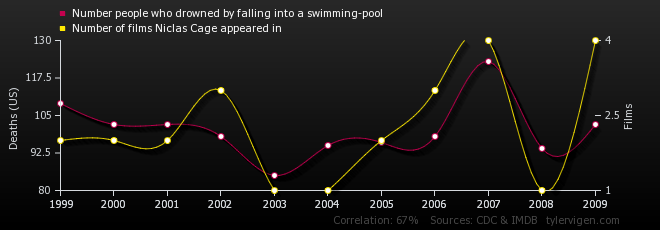
There is a strong correlation between the people who drowned by falling into the swimming pool and the number of times Nicholas Cage appeared in a movie. A high correlation (0.66 here) is found here. This doesn’t imply causation.
(for many such interesting spurious correlations check http://tylervigen.com/spurious-correlations )
How robust is the pattern?
The number of elements in a sequence/geometry and the strength of it’s a relationship if all the parts are interconnected defines the robustness of a pattern. In the first example, one can see that the elements are connected with each other by a factor of 2. Hence the pattern is robust and hence is predictable.
1, 2, 4, 8, 16, 32, 64, 128, 256
Strong linear correlations are much easier to predict. This also helps in describing the whole pattern with only a very limited amount of information. This is the key to compression.
Symmetry
One of the most fundamental organizing principle to the pattern is symmetry. Symmetry in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or, scaling. Symmetry in patterns is being studied in the area called group theory.
Symmetry has been vastly studied and it is a common belief in science and mostly in theoretical physics that practically all laws of nature originated in symmetries. (recommended interesting reading: https://arxiv.org/abs/2001.01737 and https://science.sciencemag.org/content/177/4047/393 )
Asymmetry
Whereas symmetry can be defined as above, the definition of asymmetry is the absence of symmetry. Many times relationship between asymmetric elements can lead to symmetry in a higher level of abstraction.
The study of asymmetry and symmetry helps us understand the order in a system.
Study of asymmetry and symmetry helps us understand the order in a system.
Order can thus be an arrangement of elements in relation to each other as per a particular sequence pattern or method and symmetries can be used to compress the information and help us to understand the world and defined order in it.
Imagine a sequence:
1, 2, 4, 8, 16, 32, 40, 80, 160, ___
Though one can observe a pattern, one also understands that it’s more than one pattern and both need to be specified in order to explain a system with such elements. Thus more information is required in expressing this system and it’s patterns.
1, 2, 4, 8, 16, 32, 32, 16, 8, ___
This requires lesser information and better prediction of the next few steps and gives confidence in the order of the system arising out of symmetry.
Referring to our previous sub of random walk, we can say the random sequence of events doesn’t have any order.
Thus higher the asymmetry, more is the information required to understand and describe the system. A complicated pattern would require a detailed description of the entire system to fully understand it.
In the case of a symmetrical system, once we understand the rules by which the elements are related and the symmetry, the pattern will appear relatively simple.
Read the story of the discovery of a pattern that defines us : https://phys.org/news/2018-04-convoluted-history-double-helix.html
Is the world around us asymmetric or we do not know all the patterns that exist?
This is one question that is leading to discover and unravel the mysteries of the world. From Kepler's laws to Schrodinger's equations, we had various eureka moments and were able to model the world better as we were able to find the pattern every-time we realized there is none. This is the reason for the strong belief in the physics community that the world is symmetric, just the discovery of further various patterns is still left.
(Reading recommendation: https://www.wolframphysics.org/ and https://www.wolframscience.com/ )
Complexity
noun
/kəmˈplek.sə.ti/
state of having many parts and being difficult to understand or find an answer to

Imagine an interplay of symmetry and asymmetry and they are creating a pattern that has both orders as well as randomness or chaos. This interplay is the defining feature of complexity. In most of these cases, the correlation between the element is nonlinear, sparse, and will likely change with varying degrees of the time.
Why should you care about complexity or patterns?
Patterns are something that we notice when we see it. How does nature without any kind of blueprint or design put together patterns like these? When we make patterns, it is because we planned it that way, putting the elements into place. In nature, there is no planner, but somehow natural forces conspire to bring about something that looks quite beautiful.
Understanding of complexity and pattern helps us engineer, plan, and predict outcomes. In a way exploring future while being in present. This is quite powerful.
Economist: Economists understand how important it is to predict cycles and find patterns. Most of the job of an economist is around studying these patterns and trying to find emerging trends.
https://ourworldindata.org/how-and-why-econ-complexity
Data Scientist: The recently evolved stream of data science has a considerable effort on spotting a pattern in a given set of data. Machine learning tries to use various techniques like regression etc. to find those patterns. In such analysis, models are the parameters which unravel the hidden pattern in the task when applied in a systemic way.
Sample: Word2vec or Genome project
Engineer: Engineering is an application of the patterns to build something useful. Understanding the relationship between elements helps in designing useful applications ranging from a lever to starship.
CxO : From product management to people management, CxOs life is all about navigating complexities. Systems thinking is a new word for understanding the role of elements and their correlation in all streams of their work. Successful CxOs are able to find those patterns and are able to use them to their advantage.
Sales: Nothing can be as unpredictable as sales and yet there are some who are salesmen of the year, every year! They are able to understand the interaction between the elements far better than others. This elementary supply chain game is helpful in understanding how small elements can create sequences which are difficult to predict https://beergameapp.com/
Politician and policymaker: If you are a politician or policymaker, I bet you have other things to do than to read this sub. But now that you are here, you can relate how an individual’s beliefs and their relationship with others creates a society and the impact of a policy measure on masses.
Patterns are everywhere. Despite being studied extensively, a lot is yet to be known. Finding patterns and relating it to the real world is a highly complex and unexplored world.
So the next time you see the complexities around you, you know the task is only to find patterns in it.
But does finding patterns in data also mean that data is trying to tell us something? Not always!
I am leaving you with this video to ponder further.
Presentation
..coming up soon.
Community
Through this series, I intend to build a community of scientists, researchers, and doers. If you are pursuing some interesting research and want to share it with us, please send me a message.
The idea behind the series is to share a community reading list and explore new ideas. This newsletter is a spin-off of an everyday AI session series where we pick one topic of AI a day and discussed that.
Share the sub with people you think would love to be a part of this community.



